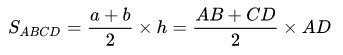Công thức tính diện tích hình thang là gì? Cách tính diện tích hình thang cân, diện tích hình thang vuông?

Nội dung chính

• Công thức tính diện tích hình thang là gì? Cách tính diện tích hình thang cân, diện tích hình thang vuông?
• Cấp trung học cơ sở, môn toán nhằm giúp học sinh đạt các mục tiêu như thế nào?
• Đặc điểm Môn Toán trong chương trình giáo dục phổ thông được quy định như thế nào?

Công thức tính diện tích hình thang là gì? Cách tính diện tích hình thang cân, diện tích hình thang vuông?

Hình thang là một loại hình tứ giác lồi thường gặp trong cả toán học lẫn trong cuộc sống thực tế. Hình thang sẽ có 2 cạnh đáy là 2 cạnh song song với nhau và 2 cạnh còn lại được gọi là 2 cạnh bên.

Diện tích hình thang được hiểu là diện tích của mặt phẳng nằm bên trong 4 cạnh tạo nên hình thang mà chúng ta có thể nhìn thấy. Có rất nhiều loại hình thang mà bạn có thể bắt gặp trong các bài tập áp dụng công thức tính diện tích hình thang như hình thang vuông, thang cân, hình chữ nhật, hình bình hành…

Dưới đây là Công thức tính diện tích hình thang, Công thức tính diện tích hình thang cân, Công thức tính diện tích hình thang vuông:

(1) Công thức tính diện tích hình thang (Công thức chung)

Trong đó:

- Diện tích hình thang: S

- Chiều cao – đường nối từ đỉnh đến cạnh đáy và vuông góc với cạnh đáy của hình thang: h

- Chiều dài 2 cạnh đáy: a, b.

(2) Công thức tính hình thang cân

Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. 2 cạnh bên của hình thang cân bằng nhau và không song song với nhau.

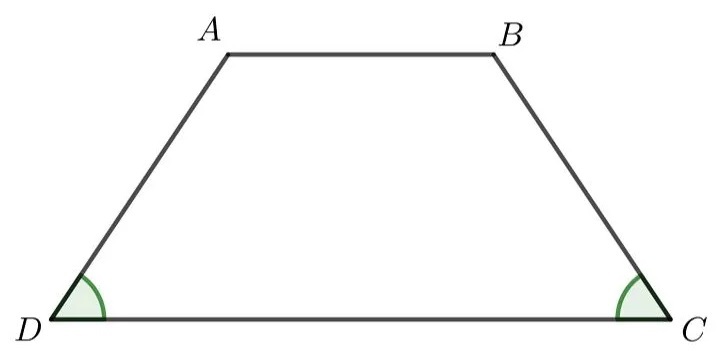
Công thức tính diện tích hình thang cân cũng tương tự với công thức chung, nhưng cũng có thể áp dụng cách chia nhỏ hình thang thành nhiều phần để tính diện tích, sau đó cộng hết lại với nhau là được.

Ví dụ: Hình thang cân ABCD có 2 cạnh bên AD và BC bằng nhau. Đường cao AH và BK, hình thang sẽ được chia ra thành 1 hình chữ nhật ABKH và 2 hình tam giác là ADH và BCK. Áp dụng công thức tính diện tích hình chữ nhật cho ABHK và diện tích tam giác cho ADH và BCK sau đó cộng tất cả diện tích để tìm diện tích hình thang ABCD.

Giải:

(3) Công thức tính diện tích hình thang vuông

Hình thang vuông cũng là một loại hình thang, nhưng hình thang này đặc biệt hơn khi chứa 2 góc vuông và một trong 2 cạnh bên vuông góc với 2 đáy.

Công thức chung tính diện tích hình thang vuông tương tự như hình thang thường: trung bình cộng 2 cạnh đáy nhân với chiều cao giữa 2 đáy, tuy nhiên chiều cao ở đây chính là cạnh bên vuông góc với cả 2 đáy.

Trong đó:

- S là diện tích hình thang.

- a và b là độ dài 2 cạnh đáy.

- h là độ dài cạnh bên vuông góc với 2 đáy.

Công thức tính diện tích hình thang là gì? Cách tính diện tích hình thang cân, diện tích hình thang vuông? (Hình ảnh Internet)

Cấp trung học cơ sở, môn toán nhằm giúp học sinh đạt các mục tiêu như thế nào?

Căn cứ theo tiểu mục 3 Mục III Phụ lục Chương trình Toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT quy định Môn Toán cấp trung học cơ sở nhằm giúp học sinh đạt các mục tiêu như sau:

- Góp phần hình thành và phát triển năng lực toán học với yêu cầu cần đạt: nêu và trả lời được câu hỏi khi lập luận, giải quyết vấn đề, thực hiện được việc lập luận hợp lí khi giải quyết vấn đề, chứng minh được mệnh đề toán học không quá phức tạp;

Sử dụng được các mô hình toán học (công thức toán học, phương trình đại số, hình biểu diễn,...) để mô tả tình huống xuất hiện trong một số bài toán thực tiễn không quá phức tạp;

Sử dụng được ngôn ngữ toán học kết hợp với ngôn ngữ thông thường để biểu đạt các nội dung toán học cũng như thể hiện chứng cứ, cách thức và kết quả lập luận;

Trình bày được ý tưởng và cách sử dụng công cụ, phương tiện học toán để thực hiện một nhiệm vụ học tập hoặc để diễn tả những lập luận, chứng minh toán học.

- Có những kiến thức và kĩ năng toán học cơ bản về:

+ Số và Đại số: Hệ thống số (từ số tự nhiên đến số thực); tính toán và sử dụng công cụ tính toán; ngôn ngữ và kí hiệu đại số; biến đổi biểu thức đại số, phương trình, hệ phương trình, bất phương trình; sử dụng ngôn ngữ hàm số để mô tả (mô hình hoá) một số quá trình và hiện tượng trong thực tiễn.

+ Hình học và Đo lường: Nội dung Hình học và Đo lường ở cấp học này bao gồm Hình học trực quan và Hình học phẳng. Hình học trực quan tiếp tục cung cấp ngôn ngữ, kí hiệu, mô tả (ở mức độ trực quan) những đối tượng của thực tiễn (hình phẳng, hình khối); tạo lập một số mô hình hình học thông dụng; tính toán một số yếu tố hình học; phát triển trí tưởng tượng không gian; giải quyết một số vấn đề thực tiễn đơn giản gắn với Hình học và Đo lường. Hình học phẳng cung cấp những kiến thức và kĩ năng (ở mức độ suy luận logic) về các quan hệ hình học và một số hình phẳng thông dụng (điểm, đường thẳng, tia, đoạn thẳng, góc, hai đường thẳng song song, tam giác, tứ giác, đường tròn).

+ Thống kê và Xác suất: Thu thập, phân loại, biểu diễn, phân tích và xử lí dữ liệu thống kê; phân tích dữ liệu thống kê thông qua tần số, tần số tương đối; nhận biết một số quy luật thống kê đơn giản trong thực tiễn; sử dụng thống kê để hiểu các khái niệm cơ bản về xác suất thực nghiệm của một biến cố và xác suất của một biến cố; nhận biết ý nghĩa của xác suất trong thực tiễn.

- Góp phần giúp học sinh có những hiểu biết ban đầu về các ngành nghề gắn với môn Toán; có ý thức hướng nghiệp dựa trên năng lực và sở thích, điều kiện và hoàn cảnh của bản thân; định hướng phân luồng sau trung học cơ sở (tiếp tục học lên, học nghề hoặc tham gia vào cuộc sống lao động).

Đặc điểm Môn Toán trong chương trình giáo dục phổ thông được quy định như thế nào?

Căn cứ theo Mục I Phụ lục Chương trình Toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT quy định đặc điểm Môn Toán giáo dục phổ thông như sau:

+ Toán học ngày càng có nhiều ứng dụng trong cuộc sống, những kiến thức và kĩ năng toán học cơ bản đã giúp con người giải quyết các vấn đề trong thực tế cuộc sống một cách có hệ thống và chính xác, góp phần thúc đẩy xã hội phát triển.

+ Môn Toán ở trường phổ thông góp phần hình thành và phát triển các phẩm chất chủ yếu, năng lực chung và năng lực toán học cho học sinh; phát triển kiến thức, kĩ năng then chốt và tạo cơ hội để học sinh được trải nghiệm, vận dụng toán học vào thực tiễn; tạo lập sự kết nối giữa các ý tưởng toán học, giữa Toán học với thực tiễn, giữa Toán học với các môn học và hoạt động giáo dục khác, đặc biệt với các môn Khoa học, Khoa học tự nhiên, Vật lí, Hoá học, Sinh học, Công nghệ, Tin học để thực hiện giáo dục STEM.

+ Nội dung môn Toán thường mang tính logic, trừu tượng, khái quát. Do đó, để hiểu và học được Toán, chương trình Toán ở trường phổ thông cần bảo đảm sự cân đối giữa “học” kiến thức và “vận dụng” kiến thức vào giải quyết vấn đề cụ thể.

+ Trong quá trình học và áp dụng toán học, học sinh luôn có cơ hội sử dụng các phương tiện công nghệ, thiết bị dạy học hiện đại, đặc biệt là máy tính điện tử và máy tính cầm tay hỗ trợ quá trình biểu diễn, tìm tòi, khám phá kiến thức, giải quyết vấn đề toán học.

+ Trong chương trình giáo dục phổ thông, Toán là môn học bắt buộc từ lớp 1 đến lớp 12. Nội dung giáo dục toán học được phân chia theo hai giai đoạn:

- Giai đoạn giáo dục cơ bản: Môn Toán giúp học sinh hiểu được một cách có hệ thống những khái niệm, nguyên lí, quy tắc toán học cần thiết nhất cho tất cả mọi người, làm nền tảng cho việc học tập ở các trình độ học tập tiếp theo hoặc có thể sử dụng trong cuộc sống hằng ngày.

- Giai đoạn giáo dục định hướng nghề nghiệp: Môn Toán giúp học sinh có cái nhìn tương đối tổng quát về toán học, hiểu được vai trò và những ứng dụng của toán học trong thực tiễn, những ngành nghề có liên quan đến toán học để học sinh có cơ sở định hướng nghề nghiệp, cũng như có khả năng tự mình tìm hiểu những vấn đề có liên quan đến toán học trong suốt cuộc đời. Bên cạnh nội dung giáo dục cốt lõi, trong mỗi năm học, học sinh (đặc biệt là những học sinh có định hướng khoa học tự nhiên và công nghệ) được chọn học một số chuyên đề học tập. Các chuyên đề này nhằm tăng cường kiến thức về toán học, kĩ năng vận dụng kiến thức toán vào thực tiễn, đáp ứng sở thích, nhu cầu và định hướng nghề nghiệp của học sinh.

+ Chương trình môn Toán trong cả hai giai đoạn giáo dục có cấu trúc tuyến tính kết hợp với “đồng tâm xoáy ốc” (đồng tâm, mở rộng và nâng cao dần), xoay quanh và tích hợp ba mạch kiến thức: Số, Đại số và Một số yếu tố giải tích; Hình học và Đo lường; Thống kê và Xác suất.