Công thức tính diện tích hình tam giác là gì? Có bao nhiêu loại tam giác? Hướng dẫn cách tính diện tích các loại tam giác?
Công thức tính diện tích hình tam giác là gì? Có bao nhiêu loại tam giác?
Công thức tính diện tích của tam giác là:
S = (a x h) / 2 |
Trong đó,
a là độ dài đáy của tam giác
h là chiều cao từ đỉnh vuông góc tới đáy của tam giác.
Để tính diện tích tam giác, ta nhân độ dài đáy với chiều cao, sau đó chia kết quả cho 2.
Dưới đây là 7 loại tam giác phổ biến:
(1) Tam giác vuông là tam giác có một góc bằng 90 độ. Hai cạnh tạo nên góc vuông được gọi là cạnh góc vuông, còn cạnh còn lại được gọi là cạnh huyền.
(2) Tam giác cân là tam giác có hai cạnh bằng nhau. Hai cạnh bằng nhau này được gọi là cạnh bên, còn cạnh còn lại được gọi là cạnh đáy.
(3) Tam giác đều là tam giác có cả ba cạnh bằng nhau.
(4) Tam giác nhọn là tam giác có tất cả ba góc nhỏ hơn 90 độ.
(5) Tam giác tù là tam giác có một góc lớn hơn 90 độ.
(6) Tam giác thường là tam giác không có cạnh và góc nào bằng nhau.
(7) Tam giác vuông cân là tam giác vừa vuông vừa cân, tức là có cả hai cạnh góc vuông và hai cạnh bên bằng nhau.

Công thức tính diện tích hình tam giác là gì? Có bao nhiêu loại tam giác? Hướng dẫn cách tính diện tích các loại tam giác? (Hình ảnh Internet)
Hướng dẫn cách tính diện tích các loại tam giác?
(1) Cách tính diện tích tam giác cân
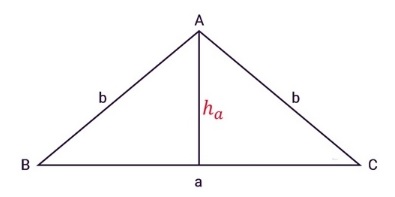
Diện tích hình tam giác cân S bằng tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, sau đó chia cho 2:
S = (a x h)/ 2 |
Trong đó:
a là chiều dài đáy tam giác cân
h là chiều cao của tam giác.
(2) Công thức tính diện tích tam giác đều
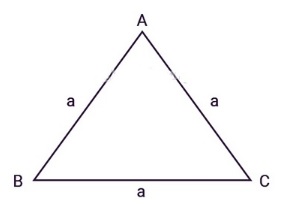
Diện tích hình tam giác đều (hay s tam giác đều) bằng tích chiều cao và cạnh đáy, sau đó chia cho 2:
S = (a x h)/ 2 |
Trong đó:
a là hiều dài đáy tam giác đều (đáy là một trong 3 cạnh của tam giác)
h là hiều cao của tam giác (chiều cao tam giác bằng đoạn thẳng hạ từ đỉnh xuống đáy)
(3) Cách tính diện tích tam giác vuông
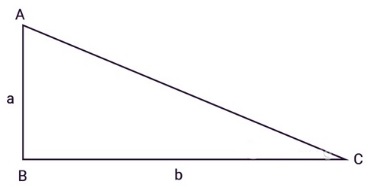
Công thức tính diện tích tam giác vuông bằng ½ tích của chiều cao với chiều dài đáy:
S = (a x b)/ 2 |
Trong đó:
a và b là độ dài 2 cạnh góc vuông.
Vì tam giác vuông có 2 cạnh góc vuông, nên chiều cao sẽ ứng với 1 cạnh góc vuông, cùng với chiều dài đáy sẽ ứng với cạnh góc vuông còn lại.
(4) Công thức tính diện tích tam giác vuông cân
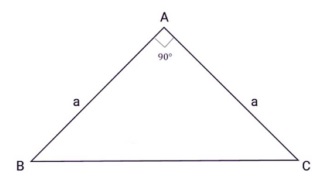
Tam giác vuông cân là tam giác vừa vuông, vừa cân. Cách tính diện tích hình tam giác vuông cân là
S = 1/2 x a^2 |
Trong đó:
Tam giác ABC vuông cân tại A
a là độ dài 2 cạnh góc vuông.
Nội dung cốt lõi môn toán học các cấp cần đạt được là gì?
Nội dung cốt lõi môn toán các cấp cần đạt được quy định tại Phụ lục ban hành kèm theo Thông tư 32/2018/TT-BGDĐT được sửa đổi bởi Thông tư 13/2022/TT-BGDĐT như sau:
Nội dung môn Toán học được tích hợp xoay quanh ba mạch kiến thức:
- Số, Đại số và Một số yếu tố giải tích;
- Hình học và Đo lường;
- Thống kê và Xác suất.
Cụ thể như sau:
Số, Đại số và Một số yếu tố giải tích là cơ sở cho tất cả các nghiên cứu sâu hơn về toán học, nhằm hình thành những công cụ toán học để giải quyết các vấn đề của toán học và các lĩnh vực khoa học khác có liên quan; tạo cho học sinh khả năng suy luận suy diễn, góp phần phát triển tư duy logic, khả năng sáng tạo toán học và hình thành khả năng sử dụng các thuật toán.
Hàm số cũng là công cụ quan trọng cho việc xây dựng các mô hình toán học của các quá trình và hiện tượng trong thế giới thực.
Hình học và Đo lường là một trong những thành phần quan trọng của giáo dục toán học, rất cần thiết cho học sinh trong việc tiếp thu các kiến thức về không gian và phát triển các kĩ năng thực tế thiết yếu.
Hình học và Đo lường hình thành những công cụ nhằm mô tả các đối tượng, thực thể của thế giới xung quanh; cung cấp cho học sinh kiến thức, kĩ năng toán học cơ bản về Hình học, Đo lường (với các đại lượng đo thông dụng) và tạo cho học sinh khả năng suy luận, kĩ năng thực hiện các chứng minh toán học, góp phần vào phát triển tư duy logic, khả năng sáng tạo toán học, trí tưởng tượng không gian và tính trực giác.
Đồng thời, Hình học còn góp phần giáo dục thẩm mĩ và nâng cao văn hoá toán học cho học sinh. Việc gắn kết Đo lường và Hình học sẽ tăng cường tính trực quan, thực tiễn của việc dạy học môn Toán học.
Thống kê và Xác suất là một thành phần bắt buộc của giáo dục toán học trong nhà trường, góp phần tăng cường tính ứng dụng và giá trị thiết thực của giáo dục toán học.
Thống kê và Xác suất tạo cho học sinh khả năng nhận thức và phân tích các thông tin được thể hiện dưới nhiều hình thức khác nhau, hiểu bản chất xác suất của nhiều sự phụ thuộc trong thực tế, hình thành sự hiểu biết về vai trò của thống kê như là một nguồn thông tin quan trọng về mặt xã hội, biết áp dụng tư duy thống kê để phân tích dữ liệu. Từ đó, nâng cao sự hiểu biết và phương pháp nghiên cứu thế giới hiện đại cho học sinh.
Ngoài ra, chương trình môn Toán học ở từng cấp cũng dành thời lượng thích đáng để tiến hành các hoạt động thực hành và trải nghiệm cho học sinh chẳng hạn như:
Tiến hành các đề tài, dự án học tập về Toán, đặc biệt là các đề tài và các dự án về ứng dụng toán học trong thực tiễn; tổ chức các trò chơi học toán, câu lạc bộ toán học, diễn đàn, hội thảo, cuộc thi về Toán; ra báo tường (hoặc nội san) về Toán; tham quan các cơ sở đào tạo và nghiên cứu toán học, giao lưu với học sinh có khả năng và yêu thích môn Toán,...
Những hoạt động đó sẽ giúp học sinh vận dụng những tri thức, kiến thức, kĩ năng, thái độ đã được tích luỹ từ giáo dục toán học và những kinh nghiệm của bản thân vào thực tiễn cuộc sống một cách sáng tạo; phát triển cho học sinh năng lực tổ chức và quản lí hoạt động, năng lực tự nhận thức và tích cực hoá bản thân; giúp học sinh bước đầu xác định được năng lực, sở trường của bản thân nhằm định hướng và lựa chọn nghề nghiệp; tạo lập một số năng lực cơ bản cho người lao động tương lai và người công dân có trách nhiệm.
Quý khách cần hỏi thêm thông tin về có thể đặt câu hỏi tại đây.









