Công thức tính diện tích hình lập phương? Diện tích xung quanh hình lập phương, Diện tích toàn phần hình lập phương?

Nội dung chính

• Công thức tính diện tích hình lập phương? Diện tích xung quanh hình lập phương, Diện tích toàn phần hình lập phương?
• Đặc điểm môn Toán theo Thông tư 32 như thế nào?
• Nhiệm vụ chung giáo dục trung học năm học 2024 2025 thực hiện như thế nào?

Công thức tính diện tích hình lập phương? Diện tích xung quanh hình lập phương, Diện tích toàn phần hình lập phương?

Hình lập phương là hình khối ba chiều có chiều rộng, dài, cao đều bằng nhau. Với 6 mặt đều là hình vuông, hình lập phương mang cũng là hình hộp chữ nhật có tất cả các cạnh bằng nhau.

Ta có quy ước sau về hình lập phương như sau:

a: Độ dài của cạnh lập phương

P: Chu vi hình lập phương

S(bm): Diện tích bề mặt hình lập phương

S(xq): Diện tích xung quanh hình lập phương

S(tp): Diện tích toàn phần hình lập phương

V: thể tích

(1) Diện tích xung quanh hình lập phương

Để tính diện tích xung quanh hình lập phương, ta lấy bình phương của một cạnh rồi nhân với 4.

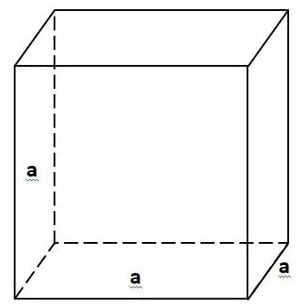
Công thức tính diện tích xung quanh hình lập phương là:

Trong đó:

a: Độ dài của cạnh lập phương

S(xq): Diện tích xung quanh hình lập phương

(2) Diện tích toàn phần hình lập phương

Để tính diện tích xung quanh hình lập phương, ta lấy bình phương của một cạnh rồi nhân với 6.

Công thức tính diện tích toàn phần hình lập phương là:

Trong đó:

a: Độ dài của cạnh lập phương

S(tp): Diện tích toàn phần hình lập phương

Công thức tính diện tích hình lập phương? Diện tích xung quanh hình lập phương, Diện tích toàn phần hình lập phương? (Hình ảnh Internet)

Đặc điểm môn Toán theo Thông tư 32 như thế nào?

Căn cứ theo Mục I Phụ lục Chương trình Toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT quy định đặc điểm Môn Toán giáo dục phổ thông như sau:

+ Toán học ngày càng có nhiều ứng dụng trong cuộc sống, những kiến thức và kĩ năng toán học cơ bản đã giúp con người giải quyết các vấn đề trong thực tế cuộc sống một cách có hệ thống và chính xác, góp phần thúc đẩy xã hội phát triển.

+ Môn Toán ở trường phổ thông góp phần hình thành và phát triển các phẩm chất chủ yếu, năng lực chung và năng lực toán học cho học sinh; phát triển kiến thức, kĩ năng then chốt và tạo cơ hội để học sinh được trải nghiệm, vận dụng toán học vào thực tiễn; tạo lập sự kết nối giữa các ý tưởng toán học, giữa Toán học với thực tiễn, giữa Toán học với các môn học và hoạt động giáo dục khác, đặc biệt với các môn Khoa học, Khoa học tự nhiên, Vật lí, Hoá học, Sinh học, Công nghệ, Tin học để thực hiện giáo dục STEM.

+ Nội dung môn Toán thường mang tính logic, trừu tượng, khái quát. Do đó, để hiểu và học được Toán, chương trình Toán ở trường phổ thông cần bảo đảm sự cân đối giữa “học” kiến thức và “vận dụng” kiến thức vào giải quyết vấn đề cụ thể.

+ Trong quá trình học và áp dụng toán học, học sinh luôn có cơ hội sử dụng các phương tiện công nghệ, thiết bị dạy học hiện đại, đặc biệt là máy tính điện tử và máy tính cầm tay hỗ trợ quá trình biểu diễn, tìm tòi, khám phá kiến thức, giải quyết vấn đề toán học.

+ Trong chương trình giáo dục phổ thông, Toán là môn học bắt buộc từ lớp 1 đến lớp 12. Nội dung giáo dục toán học được phân chia theo hai giai đoạn:

- Giai đoạn giáo dục cơ bản: Môn Toán giúp học sinh hiểu được một cách có hệ thống những khái niệm, nguyên lí, quy tắc toán học cần thiết nhất cho tất cả mọi người, làm nền tảng cho việc học tập ở các trình độ học tập tiếp theo hoặc có thể sử dụng trong cuộc sống hằng ngày.

- Giai đoạn giáo dục định hướng nghề nghiệp: Môn Toán giúp học sinh có cái nhìn tương đối tổng quát về toán học, hiểu được vai trò và những ứng dụng của toán học trong thực tiễn, những ngành nghề có liên quan đến toán học để học sinh có cơ sở định hướng nghề nghiệp, cũng như có khả năng tự mình tìm hiểu những vấn đề có liên quan đến toán học trong suốt cuộc đời. Bên cạnh nội dung giáo dục cốt lõi, trong mỗi năm học, học sinh (đặc biệt là những học sinh có định hướng khoa học tự nhiên và công nghệ) được chọn học một số chuyên đề học tập. Các chuyên đề này nhằm tăng cường kiến thức về toán học, kĩ năng vận dụng kiến thức toán vào thực tiễn, đáp ứng sở thích, nhu cầu và định hướng nghề nghiệp của học sinh.

+ Chương trình môn Toán trong cả hai giai đoạn giáo dục có cấu trúc tuyến tính kết hợp với “đồng tâm xoáy ốc” (đồng tâm, mở rộng và nâng cao dần), xoay quanh và tích hợp ba mạch kiến thức: Số, Đại số và Một số yếu tố giải tích; Hình học và Đo lường; Thống kê và Xác suất.

Nhiệm vụ chung giáo dục trung học năm học 2024 2025 thực hiện như thế nào?

Căn cứ theo Mục A Công văn 3935/BGDĐT-GDTrH năm 2024 đề ra nhiệm vụ chung cho giáo dục trung học năm học 2024 2025 như sau:

(1) Thực hiện Chương trình giáo dục phổ thông 2018 (CT GDPT 2018) đối với tất cả các khối lớp, trong đó tập trung chuẩn bị tốt các điều kiện triển khai CT GDPT 2018 đối với lớp 9, lớp 12 bảo đảm hoàn thành chương trình năm học và nâng cao chất lượng giáo dục trung học. Chuẩn bị tổ chức đánh giá tổng kết việc triển khai thực hiện CT GDPT 2018 giai đoạn 2020-2025.

(2) Thực hiện hiệu quả các phương pháp, hình thức tổ chức dạy học, kiểm tra đánh giá nhằm phát triển phẩm chất, năng lực học sinh; đa dạng hóa hình thức tổ chức các hoạt động giáo dục tích hợp phát triển các kỹ năng cho học sinh; thúc đẩy và nâng cao chất lượng giáo dục STEM, giáo dục hướng nghiệp và định hướng phân luồng học sinh sau trung học cơ sở và sau trung học phổ thông.

(3) Chú trọng thực hiện công tác phát triển mạng lưới trường, lớp; tăng cường cơ sở vật chất, thiết bị dạy học bảo đảm yêu cầu triển khai CT GDPT 2018; nâng cao chất lượng phổ cập giáo dục trung học cơ sở.

(4) Tập trung phát triển đội ngũ giáo viên và cán bộ quản lý giáo dục bảo đảm chất lượng thực hiện CT GDPT 2018; chú trọng công tác tập huấn, bồi dưỡng thường xuyên nâng cao năng lực chuyên môn, nghiệp vụ của đội ngũ giáo viên.

(5) Thực hiện hiệu quả việc quản lý giáo dục, quản trị trường học; bảo đảm dân chủ, kỷ cương, nền nếp, chất lượng và hiệu quả trong các cơ sở giáo dục trung học; tổ chức tốt các phong trào thi đua. Tăng cường công tác tư vấn, hướng dẫn, giám sát, thanh tra, kiểm tra theo thẩm quyền.

(6) Triển khai thực hiện hiệu quả, thiết thực chuyển đổi số trong dạy học và quản lý giáo dục; tập trung thực hiện chuyển đổi số trong quản lý kết quả học tập và rèn luyện của học sinh.