Công thức Đạo hàm sơ cấp, cấp cao và Đạo hàm lượng giác đầy đủ nhất lớp 11, 12 như thế nào?
Công thức Đạo hàm sơ cấp, cấp cao và Đạo hàm lượng giác đầy đủ nhất lớp 11, 12 như thế nào?
Theo Chương trình giáo dục phổ thông môn toán được ban hành kèm theo Thông tư 32/2018/TT-BGDĐT nêu rõ đạo hàm trong môn toán sẽ được giảng dạy cho những học sinh các lớp sau:
(1) Đạo hàm: Lớp 11
(2) Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số: Lớp 12
Vậy, công thức Đạo hàm sơ cấp, cấp cao và Đạo hàm lượng giác đầy đủ lớp 11, 12 thế nào?
Quy tắc tính Đạo hàm chung:
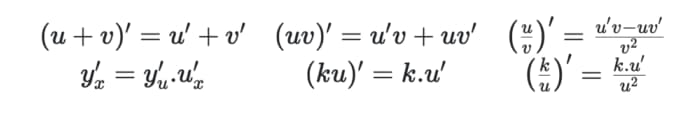
Công thức Đạo hàm sơ cấp:

Công thức Đạo hàm cấp cao:

Công thức Đạo hàm Lượng giác:

Bảng công thức Đạo hàm và nguyên hàm:
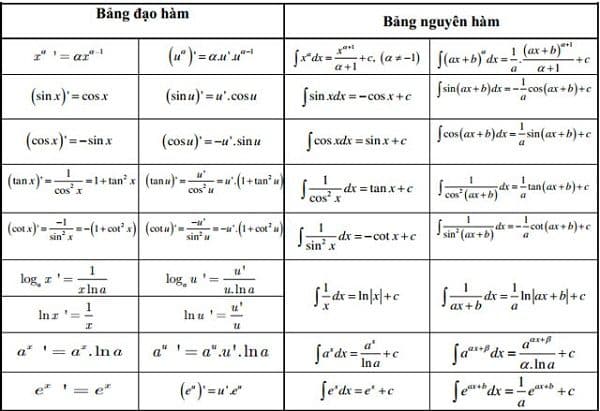
Ngoài ra, các bạn học sinh cũng có thể ghi nhớ bảng công thức đạo hàm các hàm số thường gặp như sau:


Công thức Đạo hàm sơ cấp, cấp cao và Đạo hàm lượng giác đầy đủ nhất lớp 11, 12 như thế nào?
Khi học Đạo hàm trong môn toán học sinh cần đạt được những yêu cầu như thế nào?
Căn cứ theo Chương trình giáo dục phổ thông môn toán được ban hành kèm theo Thông tư 32/2018/TT-BGDĐT nêu rõ những yêu cầu cần đạt được khi học sinh được giảng dạy đạo hàm như sau:
(1) Lớp 11:
- Đạo hàm:
+ Khái niệm đạo hàm. Ý nghĩa hình học của đạo hàm:
++ Nhận biết được một số bài toán dẫn đến khái niệm đạo hàm như: xác định vận tốc tức thời của một vật chuyển động không đều, xác định tốc độ thay đổi của nhiệt độ.
++ Nhận biết được định nghĩa đạo hàm. Tính được đạo hàm của một số hàm đơn giản bằng định nghĩa.
++ Nhận biết được ý nghĩa hình học của đạo hàm.
++ Thiết lập được phương trình tiếp tuyến của đồ thị hàm số tại một điểm thuộc đồ thị.
++ Nhận biết được số e thông qua bài toán mô hình hoá lãi suất ngân hàng.
+ Các quy tắc tính đạo hàm:
++ Tính được đạo hàm của một số hàm số sơ cấp cơ bản (như hàm đa thức, hàm căn thức đơn giản, hàm số lượng giác, hàm số mũ, hàm số lôgarit).
++ Sử dụng được các công thức tính đạo hàm của tổng, hiệu, tích, thương của các hàm số và đạo hàm của hàm hợp.
++ Giải quyết được một số vấn đề có liên quan đến môn học khác hoặc có liên quan đến thực tiễn gắn với đạo hàm (ví dụ: xác định vận tốc tức thời của một vật chuyển động không đều,...).
+ Đạo hàm cấp hai:
++ Nhận biết được khái niệm đạo hàm cấp hai của một hàm số.
++ Tính được đạo hàm cấp hai của một số hàm số đơn giản.
++ Giải quyết được một số vấn đề có liên quan đến môn học khác hoặc có liên quan đến thực tiễn gắn với đạo hàm cấp hai (ví dụ: xác định gia tốc từ đồ thị vận tốc theo thời gian của một chuyển động không đều,...).
(2) Lớp 12:
- Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số:
+ Tính đơn điệu của hàm số:
++ Nhận biết được tính đồng biến, nghịch biến của một hàm số trên một khoảng dựa vào dấu của đạo hàm cấp một của nó.
++ Thể hiện được tính đồng biến, nghịch biến của hàm số trong bảng biến thiên.
++ Nhận biết được tính đơn điệu, điểm cực trị, giá trị cực trị của hàm số thông qua bảng biến thiên hoặc thông qua hình ảnh hình học của đồ thị hàm số.
+ Giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
++ Nhận biết được giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một tập xác định cho trước.
++ Xác định được giá trị lớn nhất, giá trị nhỏ nhất của hàm số bằng đạo hàm trong những trường hợp đơn giản.
+ Khảo sát và vẽ đồ thị của hàm số:
++ Nhận biết được hình ảnh hình học của đường tiệm cận ngang, đường tiệm cận đứng, đường tiệm cận xiên của đồ thị hàm số.
++ Mô tả được sơ đồ tổng quát để khảo sát hàm số (tìm tập xác định, xét chiều biến thiên, tìm cực trị, tìm tiệm cận, lập bảng biến thiên, vẽ đồ thị).
++ Khảo sát được tập xác định, chiều biến thiên, cực trị, tiệm cận, bảng biến thiên và vẽ đồ thị của các hàm số.
++ Nhận biết được tính đối xứng (trục đối xứng, tâm đối xứng) của đồ thị các hàm số trên.
+ Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn: Vận dụng được đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn.
Mục tiêu của môn Toán trong chương trình giáo dục phổ thông giúp phát triển các năng lực Toán học nào?
Tại Chương trình toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT có nêu rõ như sau:
Mục tiêu chung
Chương trình môn Toán giúp học sinh đạt các mục tiêu chủ yếu sau:
a) Hình thành và phát triển năng lực toán học bao gồm các thành tố cốt lõi sau: năng lực tư duy và lập luận toán học; năng lực mô hình hoá toán học; năng lực giải quyết vấn đề toán học; năng lực giao tiếp toán học; năng lực sử dụng công cụ, phương tiện học toán.
b) Góp phần hình thành và phát triển ở học sinh các phẩm chất chủ yếu và năng lực chung theo các mức độ phù hợp với môn học, cấp học được quy định tại Chương trình tổng thể.
c) Có kiến thức, kĩ năng toán học phổ thông, cơ bản, thiết yếu; phát triển khả năng giải quyết vấn đề có tính tích hợp liên môn giữa môn Toán và các môn học khác như Vật lí, Hoá học, Sinh học, Địa lí, Tin học, Công nghệ, Lịch sử, Nghệ thuật,...; tạo cơ hội để học sinh được trải nghiệm, áp dụng toán học vào thực tiễn.
d) Có hiểu biết tương đối tổng quát về sự hữu ích của toán học đối với từng ngành nghề liên quan để làm cơ sở định hướng nghề nghiệp, cũng như có đủ năng lực tối thiểu để tự tìm hiểu những vấn đề liên quan đến toán học trong suốt cuộc đời.
Theo như quy định trên, mục tiêu của môn Toán trong chương trình giáo dục phổ thông giúp phát triển các năng lực Toán học gồm những thành tố cốt lõi gồm:
- Năng lực tư duy và lập luận toán học;
- Năng lực mô hình hoá toán học;
- Năng lực giải quyết vấn đề toán học;
- Năng lực giao tiếp toán học;
- Năng lực sử dụng công cụ, phương tiện học toán.
Quý khách cần hỏi thêm thông tin về có thể đặt câu hỏi tại đây.









