Cấp số nhân là gì? Tổng hợp các công thức tính cấp số nhân cơ bản chi tiết, dễ hiểu, đầy đủ nhất?
Cấp số nhân là gì?
Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.
Số q được gọi là công bội của cấp số nhân.
Nếu (un) là cấp số nhân với công bội q, ta có công thức truy hồi: un = un-1 . q với n ∈ N*
Đặc biệt:
- Khi q = 0, cấp số nhân có dạng u1; 0; 0; … 0; …
- Khi q = 1, cấp số nhân có dạng u1; u1; … u1;…
- Khi u1 = 0 thì với mọi q, cấp số nhân có dạng 0; 0; 0; … 0; …
Công thức tính cấp số nhân cơ bản chi tiết, dễ hiểu, đầy đủ mới nhất năm 2024 là gì?
Công thức truy hồi:
- Nếu (Un) là cấp số nhân với công bội q, ta có công thức truy hồi:

+ q > 1 => Cấp số nhân là dãy số tăng
+ q = 1 => Cấp số nhân là dãy số không đổi
+ 0 < q < 1 => Cấp số nhân là dãy số giảm
+ q = 0 => Cấp số nhân có dạng U1, 0, 0...
+ q < 0 => Cấp số nhân là dãy không tăng, không giảm
Công thức số hạng tổng quát:
Nếu cấp số nhân (Un) có số hạng đầu U1 và công bội q thì số hạng tổng quát Un được xác định bởi công thức:
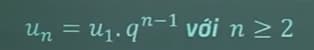
Ví dụ: Cho cấp số nhân (Un) với U1 = 3, q = -1/2
a. Tính U2020
b. Hỏi -3/512 là số hạng thứ mấy?
Hướng dẫn giải:
a. U2020 = U1 . q^2019
= 3 . (-1/2)^2019
b. Un = U1 . q^(n-1)
⇔ -3/512 = 3.(-1/2)^(n-1)
⇔ -1/512 = (-1/2)^(n-1)
⇔ (-1/2)^9 = (-1/2)^(n-1)
=> 9 = n -1
=> n =10
Vậy số hạng thứ 10 là số -3/512
Ví dụ 2: Tế bào E coli trong điều kiện nuôi cấy thích hợp cứ 20p lại phân đôi một lần.
a. Hỏi một tế bào sau 10 lần phân chia sẽ thành bao nhiêu tế bào?
b. Nếu có 10^5 tế bào sau 2 giờ sẽ phân chia thành bao nhiêu tế bào?
Hướng dẫn giải:
q=2
a. Sau lần phân bảo đầu tiền: U1 = 2 tế bào
Sau 10 lần thì sẽ có:
U10 = U1 . q^9 = 2 . 2^9 = 1024 tế bào
b. 2 giờ = 120 phút => 6 lần
Sau 1 lần phân bào sẽ có:
U1 = 2. 10^5 tế bào
Sau 6 lần phân bào sẽ có:
U6 = u1. q^5 = 2. 10^5 . 2^5
= 2^6 . 10^5 tế bào

Cấp số nhân là gì? Tổng hợp các công thức tính cấp số nhân cơ bản chi tiết, dễ hiểu, đầy đủ nhất? (Hình từ internet)
Có các dạng bài tập về cấp số nhân nào?
Cấp số nhân có nhiều ứng dụng trong thực tế như trong tài chính, kinh tế, khoa học máy tính, xử lý tín hiệu, và nhiều lĩnh vực khác. Ví dụ, trong tài chính, cấp số nhân được sử dụng để tính lãi suất lũy tiến; trong khoa học máy tính, nó được áp dụng trong các thuật toán tối ưu và mã hóa thông tin.
Theo đó, có các dang bài ta
Dạng 1: Nhận biết CSN
Bước 1: Tính q=un+1un,∀n≥1
Bước 2: Kết luận:
+ Nếu q là số không đổi thì dãy (un) là CSN.
+ Nếu q thay đổi theo n thì dãy (un) không là CSN.
Dạng 2: Tìm công bội của cấp số nhân
Sử dụng các tính chất của CSN, biến đổi để tính công bội của CSN.
Dạng 3: Tìm số hạng của cấp số nhân
Sử dụng công thức tính số hạng tổng quát un=u1.qn–1,n≥2
Dạng 4: Tính tổng cấp số nhân của n số hạng đầu tiên trong dãy
Để tính tổng của CSN với n số hạng đầu tiên trong dãy số, ta sử dụng công thức:
Sn=u1+u2+…+un=u1(1–qn)1–q
Dạng 5: Tìm CSN
+ Tìm các yếu tố xác định một CSN như: số hạng đầu u1, công bội q.
+ Tìm công thức cho số hạng tổng quát un=u1.qn–1,n≥2.
Môn Toán trong chương trình giáo dục phổ thông 2018 giúp phát triển các năng lực Toán học nào?
Tại Chương trình toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT về chương trình giáo dục phổ thông có nêu rõ như sau:
Mục tiêu chung
Chương trình môn Toán giúp học sinh đạt các mục tiêu chủ yếu sau:
a) Hình thành và phát triển năng lực toán học bao gồm các thành tố cốt lõi sau: năng lực tư duy và lập luận toán học; năng lực mô hình hoá toán học; năng lực giải quyết vấn đề toán học; năng lực giao tiếp toán học; năng lực sử dụng công cụ, phương tiện học toán.
b) Góp phần hình thành và phát triển ở học sinh các phẩm chất chủ yếu và năng lực chung theo các mức độ phù hợp với môn học, cấp học được quy định tại Chương trình tổng thể.
c) Có kiến thức, kĩ năng toán học phổ thông, cơ bản, thiết yếu; phát triển khả năng giải quyết vấn đề có tính tích hợp liên môn giữa môn Toán và các môn học khác như Vật lí, Hoá học, Sinh học, Địa lí, Tin học, Công nghệ, Lịch sử, Nghệ thuật,...; tạo cơ hội để học sinh được trải nghiệm, áp dụng toán học vào thực tiễn.
d) Có hiểu biết tương đối tổng quát về sự hữu ích của toán học đối với từng ngành nghề liên quan để làm cơ sở định hướng nghề nghiệp, cũng như có đủ năng lực tối thiểu để tự tìm hiểu những vấn đề liên quan đến toán học trong suốt cuộc đời.
Theo như quy định trên, mục tiêu của môn Toán trong chương trình GDPT 2018 giúp phát triển các năng lực Toán học như sau:
- Năng lực tư duy và lập luận toán học;
- Năng lực mô hình hoá toán học.
Quý khách cần hỏi thêm thông tin về có thể đặt câu hỏi tại đây.









